
Beklenen kar nihayet başladı. Dışarıda kar yağıyor. Vali Bey okulları tatil etti. Bu da beklenen haberdi!
Parklarda bahçelerde kaldırım kenarlarında taze karın keyfini çıkaran çocuklar, neşe içinde “Vali’ye selam, tatile devam!” sloganları atıyorlar. Evlerden çık(a)mayanlar, arabaların camlarına takılan vantuzlu minik peluş ayıcıklar gibi pencerelere yapışmışlar, yutkuna yutkuna dışarıda oynayanları seyretmekteler...
Bundan neredeyse 30 sene kadar önceydi. Okula gitmek üzere yataklarımızdan kalktığımızda, kendimizi bembeyaz bir uzayın ortasında bulmuştuk. Kar bütün gece aralıksız yağmıştı ve hâlâ öyle yağıyordu. Annem, “Bu havada okula gidilmez!” dedi. Fakat okulların tatil edildiğine dair bir haber de yoktu. Olsa da nasıl bilecektik?
O zamanlar okulların tatil olduğunu öğrenmenin tek yolu, okula kadar gidip, gerisin geri dönmekti.
Biz iki kardeş, her zamankinden daha sıkı kat kat giyindirilerek, bu beyaz uzayın içine, imkânları son derece kıt bir ülkenin gariban astronotları gibi salınıverildik. Fırtınalı tipinin ağzımıza burnumuza doldurduğu kar tanelerini yalaya yuta, beş karış karla kaplı daracık sokaklardan kaya yuvarlana okul yoluna revan olduk.
Tipi her yanı sardı. Bir ara sokak başındaki elektrik direğine asılı hoparlörden bir ses duyar gibi olunca, durduk.
– Tikkat! Tikkatışşhşhışşş..
– Ne diyo la?
– Ne ne diyo?
– Hapöller ne diyo?
– Ne diyo?
– Sus bak sus!
– Tikkat! Tikkat! Hışırrrtıss... De! Ne! Me! Se! Se! Ses! Mıhtar gonuşuyo! Se! Se! Sessshışşşşş.. Gorkmaaa sönmeeeez! Gorkmahışşş.. Se! Se! Ses! De! Ne! Me! Gorkmahışşş...
– Muhtarın sesi!
– Hava muhalefetinden ötürüşşhışşşhaşırıt! Tikkat Tikkat! Mıhtar gonuşşşşşşhışşşşş...
– Ya yürü ya!
– Atkın açılmış la!
– Örtsene..
– Dön!
– Çorabım ıslandı!
– Benim de.
– Hava çok serin!
– Ne serini, soğuk!
– Tikkat Tikkat! Mıhtar gonuşşşhışşşş...
– Dinle! Dinle!
– Ses! Ses! Sesssssshışşşşşşş...
– Yürü ya geç kaldık zaten yürü!
– Kulaklarım duruyo mu la?
– Niye durmasın?
– Bilmem! Bana durmuyomuş gibi geliyo!
–Tikkat Tikkat! Mıhtar! Mıhşşhışş... De! Ne! Me! Se! Se! Ses! Gorkmaaa sönmeeeez! Se! Se! Ses! De! Ne! Me! Gorkmahışşş...
– Soğuktandır!
– Huh! Huh! Parmaklarım dondu!
–Tikkat Tikkat! Mıhtar! Mıhşşhışş... Hava muhafeletinden ötürü... Hışırıt hışırıt.. Okullar tatil edilmiştir! Tikkat Tikkat! Ses! Ses gontrol! Gorkmaaa sönmeez! Gorkmaaaa! Alo! Alo! Mıhtar gonuşuyo! Mıhtar! Mıhtar! Hava
muhafeletinden ötürü okullar üç gün tatil edilmiştir. Ses! Ses! Ses kontrohışşşşışşşıhş...
– Aha! Okullar iptal! Hem de üç gün!
– Kardan adam yapalım, kardan adam!
– Kardan adam!
– Kardan adam!
– Kardan adam!
Ve otuz küsür yıl geçti aradan.
O gün yaptığımız kardan adamlar ay sonuna varamadan eridi. Yol kenarlarındaki dere yollarından, ışıltılı bir şırıltı ile akıp gitti. Buhar olup, dünyanın müthiş su döngüsüne karıştı ve kimbilir kaç defa, yeryüzüne yeniden kar olarak iniverdi...
Eğer hiçbir kar tanesinin bir diğerine benzemeyecek şekilde yaratıldığını bilmeseydim, az evvel penceremin kenarına usulca bir tüy gibi konuveren yüzlerce kristal çiçekten bir kaçı ile otuz küsur yıl kadar önce tanışmış olabileceğimi söyleyebilirdim...
Ama bir kar tanesi hem benzersizdir hem de donmuş bir su zerreciğinden çok daha fazlasıdır.

Eğer ona yeterince yakından bakabilirseniz ilk bakışta muhteşem kristal bir çiçek görürsünüz. Bu küçük mucizenin, kısalı uzunlu pek çok kola sahip, simetrik mükemmel bir geometrik şekli vardır. Ve bütün bu minik kollar ve uzantılar öyle gelişigüzel, rastgele ve tesadüfen kar taneciğinin orasından burasından çıkmış ve uzamış da değildir. Her bir uzantının ve her bir uzantıdan çıkan daha küçük uzantıların—tıpkı ağaç dallarındaki gibi—hassas bir oranı vardır.
Yeryüzünün canlı cansız her bir şeyini inceleyip araştıran fizikçisinden biyoloğuna kadar bütün bilim adamlarının, neredeyse her baktıkları yerde karşılarına çıkan bu orana, matematikçiler, mimarlar, ressamlar ve heykeltraşlar ALTIN ORAN ya da benim daha çok sevdiğim, DIVINA PROPORTIONE adını verirler.
Divina Proportione; yani İLÂHÎ ORAN...

Dünyanın en acayip sayısı: Fi Sayısı
Bir sepette 20 elma, öteki sepette ise 5 armut varsa ve bize elmaların armutlara olan “oranı” soruluyorsa, tek yapmamız gereken, elmaların sayısını, armutların sayısına bölmektir. Evet bunu yapabiliriz; elma ile armut toplanmaz ama bölünebilir. Tabii sadece sayıları...
E/A= Elmalar ile armutların oranı’dır.
Bu da 20/5=4’dür. Ve 4 sayısı elmaların armutlara oranıdır.
Oran, en basit şekliyle böyle bir şeydir işte. İki çokluğun birbirlerine bölünerek aralarında kaç kat fark olduğunu bulmaktır!
Leonardo Fibonacci’nin tuhaf bir tavşan bilmecesini çözeyim derken bulduğu o ilginç sayı dizisinin gerçekten şaşırtıcı bir başka yönü ise birbirlerine olan oranlarıdır.
Eğer bir Fibonacci sayısını, kendisinden önceki Fibonacci sayısına bölerseniz aralarındaki oranı bulursunuz.
01/1=1
02/1=2
03/2=1,5
05/3=1,66666...
08/5=1,60000...
13/8=1,62500...
Fibonacci sayıları ilk üç beş tanesi hariç diğerleri birbirlerine elma ve armutlar gibi tam olarak bölünemediği için, elde edeceğimiz sayı bir İRRASYONEL yani “akıl almaz” sayıdır.
Bu derginin sonuna kadar her satırı o sayının rakamları ile doldurabiliriz. Çünkü bir sonu yoktur.
O yüzden virgülden sonra sadece beş sayıyı yazmakla yetinelim.
21/13=1,61538...
34/21=1,61904...
55/34=1,61764...
89/55=1,61818...
144/89=1,61797...
233/144=1,6180...
377/233=1,6180...
610/377=1,6183...
987/610=1,6180...
Daha fazla uzatmadan size göstermek istediğim şeyi söyleyeyim: Bundan sonra yapacağımız bütün oran hesaplarında çıkan sonuç şu değişmez sayılar ile başlayacaktır: 1,618
Mesela, F100/F99 (yani 100. Fibonacci Sayısı’nın 99. Fibonacci sayısına oranı şöyledir:
1,618033988749894848204586....
1,618’e Fİ SAYISI (ϕ ya da τ=Tau) adı verilir ve belki bir başka irrasyonel sayı olan 3,1416, yani Pi SAYISI (π) kadar ünlü değildir ama en az onun kadar şaşırtıcıdır!
Anlaşıldı! Bir çift tavşan bir odaya kapatılırsa çok çok on ay sonra bir önceki aydan yaklaşık 1,618 oranında bir üreme hızı ile çoğalırlar.
Peki Fİ SAYISI’nın bütün numarası bundan ibaret midir? Buraya kadar sizi bunun için mi çağırdım!?
Divina Proportione
Leonardo Fibonacci’nin meşhur sayı dizisini bulmasından 1500 sene kadar önceydi. Yunanlı Matematik üstadı Eukleides, (Biz onu genelde Öklid olarak tanırız) bir doğru parçasını en güzel, en cazip ve göze en hoş görünen noktasından bölmek için bir formül üzerinde çalışıyordu.
Sıradan grafik tasarımcıların bir kitap kapağı, bir poster ya da işte bunlar gibi her hangi bir şey tasarlarken sık sık başvurdukları bir yöntem vardır; eğer akıllarına ilginç bir tasarım fikri gelmiyorsa—ki genelde gelmez—her şeyi ya yukarıdan aşağıya, ya da yan yana ortalayıp, işi oldu bittiye getirirler. Bundan sonra yapmaları gereken, ne kadar mükemmel bir tasarım yaptıklarına herkesi inandırmaktır!
Öklid, sıradan bir Matematikçi olsaydı her halde “Bir doğru parçasını bölmenin en iyi yolu tam ortadan bölmektir” derdi. “Hem böylece onu iki kişi arasında hır gür çıkmadan rahatlıkla pay edebilirsiniz!”
Ancak Öklid sıradan bir Matematikçi değildi. Ve her hangi bir doğruyu en güzel şekilde bölmenin ilginç bir formülünü bulmuştu.
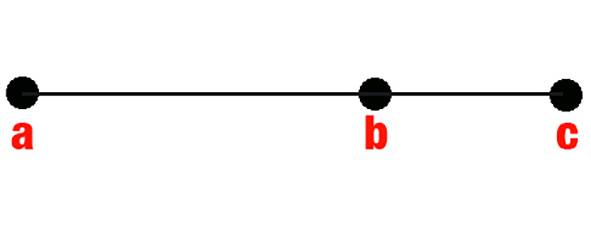
Yukarıda gördüğünüz doğru parçası, A ve B noktaları arasındaki C noktasından bölünmüş. Bu C noktası doğrunun her hangi bir noktası değil. AB’nin AC’ye oranı, yani AB/AC, AC’nin BC’ye oranına eşit. Yani:
AB/AC=AC/BC
Kısaca Öklid, AB doğrusunu öyle bir C noktasından bölmüş ki, doğru parçasının AC’ye oranı ile AC’nin BC’ye oranı aynı.
Peki bu oran ne kadardır biliyor musunuz?
1,618’dır. Yani Fİ SAYISI!
Eğer bir doğruyu, parçaları 1,618 oranına denk gelen noktadan bölerseniz şunu elde edersiniz:
AB/AC=AC/BC=1,618
…
Fi Sayısı sizi ne kadar heyecanlandırdı bilemiyorum. Ama, “Geometrinin iki büyük hazinesi vardır; biri Pisagor Teoremi, diğeri, bir doğrunun Altın Oran’a göre bölünmesidir” dediğine göre Kepler’i çok heyecanlandırmış olmalı!
Bir kez daha karşımıza çıkan bu ilginç sayı 1,618, sadece Öklid tarafından ve sadece bir doğru parçasını acayip bir yerinden bölmek için kullanılan bir oran değildi...
1,618 yani Fi, Filozoflar, matematikçiler, sanatçılar hatta müzisyenler için de çok önemli bir sayıydı.
Ona, ALTIN ORAN ismini verdiler. Garip bir şekilde insan gözü, altın oranı diğer oranlardan daha güzel ve uyumlu görüyordu.
İnsanlara hoş görünecek bir sanat eseri ortaya koymak isteyen, ‘altın oran’a dikkat etmeliydi.
Eski Yunan mimarisinin en büyük eseri olan Pertanon Tapınağı, altın oran ilkelerine göre inşa edilmişti. Yunanlıların meşhur heykeltraşı Phidias, eserlerini altın orana göre yapıyordu. Bütün Rönesans ressamları, en meşhur tablolarında altın orana dikkat ederlerdi. Bir ressam, hayalindeki kompozisyonu boş tuvallere oturtmadan önce altın oran kaidelerine göre bir plân yapar ve işe öyle koyulurdu. Leonardo da Vinci, en meşhur eserlerini mesela Mona Lisa ve Son Yemek tablolarını altın oran ilkelerine göre yapmıştı.
Yeryüzündeki en muhteşem yapılar, hep altın oran kaidelerine göre tasarlanmaktaydı. Kapıların, pencerelerin, duvarların, kulelerin ve bahçelerin boyları ile enleri arasında mutlaka altın oran bulunmaktaydı...
Muhteşem Sinan, Süleymaniye ve Selimiye’nin minarelerinde altın oranı kullanmıştı...
İnsanların severek sahiplenmek istedikleri ürünler de, yine altın orana uyumlu tasarlanmaktaydı... Cep telefonları, otomobiller, kapılar, pencereler, saatler, bilgisayar ekranları, kitap kapakları, afişler posterler... aklınıza ne geliyorsa, gözünüze—sebebini anlayamasak da—güzel görünen her şeyin, mutlaka altın orana uyan bir tarafı bulunuyordu...
Büyük dâhi Leonardo da Vinci’nin Matematik hocası Luca Pacioli, ‘Altın Oran’a öyle bir saygı duyuyordu ki, onunla ilgili yazdığı kitaba DIVINA PROPORTIONE adını koymuştu.
Divina proportione, yani İLÂHÎ ORAN!
…
Sanatlı bir eser yapmak istiyorsanız—insanların hoşuna giden, dengeli ve güzel görünen bir eser—bu bir heykel de olabilir, bir mabet de, bir tablo da, bir çikolata kutusu da... mutlaka bu oranı göz önünde bulundurmanız gerekiyordu.
Peki ama niçin?
Çünkü altın oran, yeryüzünün sanat ve güzellik ölçüsüydü. Onu insan gözü için bu kadar sıcak ve hoş gösteren buydu!
Elbette yaratılmış her şeyin bir ölçüsü vardı ve insanlar bunların bazılarını keşfedebilmişlerdi.
Altın oran, işte o keşfedilmiş ölçülerden belki de en hayret edilecek olanlarından birisiydi...
1,618 yani Fi, (ϕ) ama daha çok (τ) sembolü ile gösterilen bu şaşırtıcı rakam, Fibanocci sayıları gibi hiç ummadığımız yerlerde karşımıza çıkmaktaydı. Belki farkına varamıyorduk ama Allah’ın kâinatındaki güzellikleri görmek ve keşfetmek, gözlerimizi terbiye ediyor ve Yaratılış harikalarındaki oranlara uygun yapılmış şeyler gözümüze güzel geliyordu...
Luca Pacioli, altın orana İLÂHÎ ORAN demekle son derece haklıydı. Çünkü insanın kendi yaratılışı ve içinde yaşadığı bu büyük ev yani kâinat, altın orana göre yaratılmış sayısız örnekle doluydu.
Altın Oran, parmaklarımız arasında
Durun! Okumayı bırakın ve işaret parmağınıza bir bakın. Her zaman kendisi dışında bir şeylere işaret eden bu “işaret parmağı” bu sefer kendisine işaret etsin.
İşaret parmağı 3 boğumludur. Parmağın tam boyunun ilk iki boğuma oranı ALTIN ORAN’dır. Orta parmağın, serçe parmağa oranı da ALTIN ORAN’dır. İşin bir garip yanı da şudur: 2 elin, bütün parmakları 3 boğumludur. Her elde 5 parmak vardır. Ancak bunlardan sadece 8 tanesi ALTIN ORAN’A göre yaratılmıştır: 2,3,5,8 ise, Fibonacci Sayıları’ndandır...
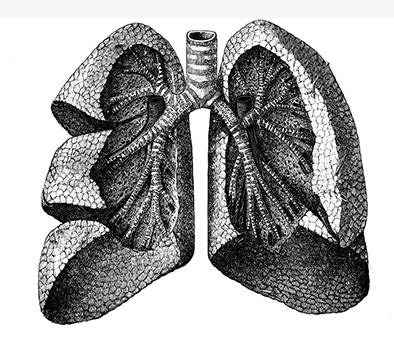
Altın Oran, ciğerimize işle(n)miş
Amerikalı bir fizikçi ile bir doktorun 80’li yılların sonlarına doğru yaptıkları bir araştırmanın sonucu, ALTIN ORAN’ın ciğerlerimizin en küçük köşesine kadar geçerli olduğunu gösterdi.
B. J. West ve A. L. Goldberger adındaki bu iki bilim adamı, akciğerleri oluşturan bronş ağacının ilk bakışta görünen asimetrik yapısının öyle tesadüfen, öyle kendi kendine ve öyle rastgele olamayacağını gördüler.
Soluk borusu akciğerlere doğru iki ana kola ayrılmaktadır. Bu kollardan soldaki sağdakinden daha kısadır. Bilmem söylemeye gerek var mı ama bu iki dalın birbirine oranı ALTIN ORAN’dır. Dahası, bütün bir akciğer yapısı içinde bu dallanma en küçük odacığa kadar sürer gider ve her bölünme ALTIN ORAN’a göre yaratılmıştır.
Matematik varsa, tesadüf yoktur!..
Eğri büğrü hudutlar

Yukarıda gördüğünüz iki noktayı en kısa yoldan birleştirmek isterseniz aralarına dosdoğru düz bir çizgi çizmeniz yeterli olacaktır. Zaten hepimize ilkokulda öğretilen bir Matematik terimi olarak ‘doğru’nun tarifi; “iki nokta arasındaki en kısa yol” şeklindedir.
Evet doğru! Doğru, iki noktayı birleştirmenin, en kısa yoludur. Ama asla tek yolu değildir. İki noktayı birleştirmenin sonsuz sayıda yolu vardır...
Ben az önce “sonsuz sayıda” mı dedim!? “Sayısız” da diyebilirdim oysa!
Doğru, bu sayısız yol arasında; kolaydan zora doğru bir sıralama yapıldığında en kolayı ve en basiti, kısadan uzuna doğru bir sıralamada ise en kestirme olanıdır.
Pablo Picasso, bir kağıt üzerindeki iki noktayı birleştirmek isteyip de, bunun için en kolay ve en kestirme yolu yani ‘doğru’yu seçseydi o da düz bir çizgi çizecekti. Ama kimsenin bu ‘doğru’ için milyonlarca lira vereceğini ya da onu görmek için müzelere gideceğini beklemeyin.
Çünkü, Picasso’nun ‘doğru’suyla sizin ‘doğru’nuz arasında en küçük bir fark bile olmayacaktı! Düz bir çizgiden ibaret olan doğru, sadece düz bir çizgi olarak kalacak ve üzerinde kendisini çizene dair,—‘herhangi birinin çizmiş olduğu’ gerçeğinden başka—hiçbir bilgi taşımayacaktı. Düz bir çizgiye bakıp, onu kimin çizdiğini söyleyemezsiniz çünkü... Sadece birinin çizmiş olduğunu söyleyebilirsiniz!
İki noktayı birleştirmenin diğer yolları ise ‘eğri’dir. Ve eğri, eğrilip büküldükçe, kendisini çizen hakkında bir ‘doğru’nun taşıyamayacağı kadar çok iz taşır. Çünkü eğri, bir tercihtir. Düz çizginin eğilip bükülmesi bir anlam ifade etmek içindir.
Kağıt üzerindeki iki noktayı birleştiren çizgi, eğilip bükülür ve bir harf olur, bir kalp olur, bir çiçek olur, bir dağ olur, bir imza olur..
İki noktayı birleştirmenin sonsuz ihtimalleri içinde, kendisini çizenin; sanatkârlığına, iradesine, hikmetine, bilgisine, vermek istediği mesaja göre her türlü şekli alabilir, çizilmiş olmaktan başka, çizeni hakkında, kitaplar dolusu bilgi verir. Bir Picasso boğası, bir Hafız Osman Vav’ı gibi, iki nokta arasında bir şaheser olur.
Doğrusu doğru yok eğri var!
Modern Matematikçiler, “aslında doğru diye bir şey yoktur” derler. “Bizim doğru dediğimiz şey, çapı sonsuz bir dairenin yay kesitinden ibarettir.”
Matematikçilerin doğru hakkındaki bu görüşlerinin dayanağı bütün bilimler gibi Matematiğin de ilham kaynağı olan, içinde insan zekâsının gezindiği şu muhteşem kâinattır. Ve bizim bu büyük evimizde, ne düz bir şekil ne de dümdüz bir hareket vardır. Oysa Galileo ve Newton’dan günümüze kadar birçok Fizikçi, hareketin düz ve mekanik bir eşitlikte meydana geldiğini söylemekteydiler. Fakat asıl gerçek, evrendeki hiçbir şeyin dümdüz bir doğrultuda ilerlemediğidir.
Her şey, büyürken gelişirken, uzarken genişlerken eğri büğrü hatlarla kuşatılır. Kendisini oluşturan zerreler sanki etrafında görünmeyen bir kalıp varmışçasına, bu eğri büğrü hatlara gider ve nihayet durmaları gereken yerlerde dururlar.
Bu tayin edilmiş yani belirlenmiş miktarlar boyunca eğrilikler, asla eğreti değildir. Bir gül goncası, bir bebeğin yanağı, bir elin beş parmağı, bir koçun boynuzları, bir filin hortumu, bir asmanın çubuğu.. yaratılmış her şey, kendine has eğrilip bükülmeleriyle nasıl olmaları gerekiyorsa öyle olurlar. Eğrilip büküldükçe de, onları bir eğip büken olduğunu, kendilerini oluşturan zerreleri adedince gösterirler...
Her şeyin tayin edilmiş bir miktarı vardır. Ve biz bu tayin edilmiş, sınırları çizilmiş miktara, kader adını veririz.
Bütün kıvrımlarda, büyülü kavislerde, bazen bir kartalın pençeleri gibi sivri çıkıntılarda, bazen bir atın akıtmalı alnı gibi mükemmel biçimlerde, bir timsahın pütürüklü sırtında, bir alabalığın kaygan derisinde, yaşlı zeytin ağaçlarının eğilip büküldükçe daha da güzelleşen dalları arasında ve bir gül yaprağının, mis kokulu kadifeden teninde, sanatkârının imzasını taşıyan, eğri büğrü ama asla eğreti olmayan bir kaderdir bu...

Eğrilerin en güzeli: Sarmal
19. yüzyıl doğa bilimcisi Alfred Russel, bir salyangozun kabuğunu örnek göstererek, “Bu şekil var olan en güzel eğridir” der.
İngiliz estetikçi William Charlton’un ifadesiyle, sarmallar “İnsanların hoşuna gider. Çünkü, bir sarmalı izlemek kolaydır.”
Bir başka doğa bilimcisi olan, Theodore Cook, Yaşamın Kavisleri adlı kitabını, bu olağanüstü güzel şekli organik tabiatta bakıp da göremediğimiz hiçbir yer olmadığını anlatmaya adamıştır, yaklaşık bir asır kadar önce.
Theodore Cook’un dediği kadar vardır gerçekten; sarmalları her yerde görürüz.

Kâinata nasıl bakıyor olursanız olun; ister teleskopla bakın, ister mikroskopla, isterseniz çıplak gözle! Baktığınız her yerde mutlaka bir sarmal görürsünüz! Her bir hücremizde taşıdığımız bütün özelliklerin; saç rengimizden ayakkabı numaramıza kadar bizi biz yapan her bilginin kayıtlı olduğu DNA olağanüstü bir sarmaldır mesela... Gökyüzündeki evimiz Samanyolu Galaksisi, hepinizin bildiği gibi muhteşem bir sarmaldır...

DNA sarmalını ve Samanyolu Galaksisi’ni hiçbirimiz çıplak gözle göremeyiz elbette ama hepimizin bir deniz minaresini görmüşlüğü vardır.

Deniz minareleri ve pek çok kabuklu deniz yumuşakçasının sırtında gezdirdiği biricik evi mükemmel birer sarmaldır. Özellikle de Odalı Nautilius, kusursuz spiral kabuğu ile, yalnız bilim adamlarının değil, mimarların, tasarımcıların ve ressamların bile hayranlığını kazanmış bir deniz kabuklusudur.
Siz hayatınızda hiç gerçek bir “odalı Nautilus” görmediniz mi? Fakat çam kozalaklarını görmüşsünüzdür!
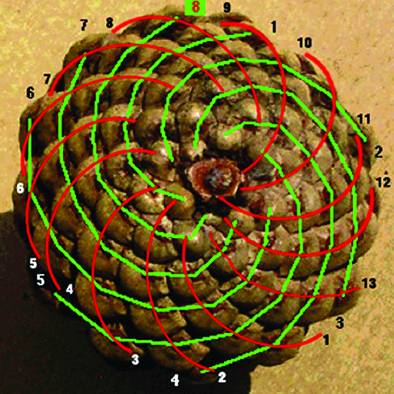
Kozalaklar da harika sarmal yapıları ile sarmallara en güzel örneklerden biridir. Spiral eğriliklerin ya da sarmalların tabiatta var olan neredeyse her şeyde karşımıza çıkmaları, onlara dikkat kesilmemiz için yeterince sebep değil midir?
…
Şu işe bakın! Tavşan hesabından yola çıkıp nerelere kadar geldik. Matematik, ne şaşırtıcı ve ne heyecanlı bir şeydi böyle! “Ayakkabılarını çıkarmadan yirmiye kadar saymak”tan çok daha fazlasıydı! Sayılar, denklemler ve türlü hesaplar arasında, bir hücrenin çekirdeğinden, Samanyolu’na kadar kâinatın her bir köşesine yayılmış sırlar vardı. Ama görmek isteyen herkese apaçık görünen sırlardı bunlar!
Matematiğin olduğu yerde tesadüf yoktu ve matematiğin olmadığı yer diye bir yer de bu kâinatta yoktu. Çünkü her şey, ince bir ölçü ve hassas bir hesap ile yaratılıyordu...
Altın dikdörtgen ve sarmallar
Altın Oran’ın göze gerçekten hoş göründüğünü anlamanın en kolay yolu bir ALTIN DİKDÖRTGEN çizmektir. Peki bir altın dikdörtgen nasıl çizilir? Önce bir miktar altın mı bulmak gerekir?
Altın dikdörtgen bu ismini uzun kenarı ile kısa kenarı arasındaki altın ‘oran’dan alır. Yani bir altın dikdörtgenin uzun kenarı ile kısa kenarı arasındaki oranı: 1,618’dir.
Ve bir altın dikdörtgen çizmenin en kolay yolu işe bir kare çizmekle başlamaktır. Bildiğiniz sıradan bir kare yani bütün kenarları birbirine eşit... Önce bir kare çizelim, sonra bu kareyi iki eşit parçaya bölelim.
Dikdörtgenlerin ortak kenarına pergelimizi koyalım ve karşı köşeye değecek bir yay çizelim ve karenin tabanını yayı kesecek kadar uzatalım.
Ve yeni şeklimizi bir dikdörtgene tamamlayalım:

İşte bu elde ettiğimiz ve daha rahat görebilmek için griye boyadığımız dikdörtgen bir ALTIN DİKDÖRTGENDİR! Uzun kenarının kısa kenarına oranı 1,618’dir. Yani ALTIN ORAN!
Peki size bu altın dikdörtgeni neden çizdirdim ben. Bir altın dikdörtgen ne işimize yarayacak? Daha da önemlisi, altın dikdörtgenin, sarmallar ile ne alâkası var?
Bunu görmek için yine bir altın dikdörtgen çizelim:

Bu mükemmel altın dikdörtgenin içinde, tek bir çizgi ile her bir kenarı altın dikdörtgenin kısa kenarı kadar olan bir kare ayıralım.
Karenin dışında kalan alan yine bir altın dikdörtgen olacaktır!
Ve biz bu altın dikdörtgenin içine de bir kare çizelim. Elbette yine kısa kenarı ölçü alarak.
Geriye kalan minik dikdörtgen tahmin edeceğiniz gibi yine bir altın dikdörtgendir.
Yani uzun kenarı ile kısa kenarı arasındaki oran 1,618’dir. Aynı işlemi bir kez daha tekrar edelim.
Bu minik altın dikdörtgenimizin içine de bir kare çizelim.
İşte ortaya bir küçük altın dikdörtgen daha çıktı. Aynı işlemi bir kez daha tekrarlayalım.
Ve bir kez daha... Gördüğünüz gibi her seferinde ortaya bir öncekinden daha küçük başka bir altın dikdörtgen çıkıyor!
Bir kez daha ve bir kez daha...
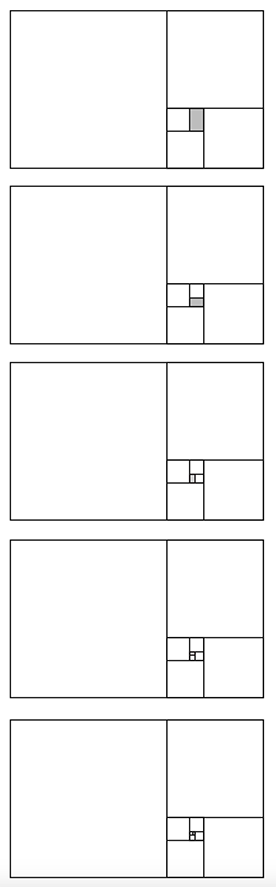
Teorik olarak bu işlemi sonsuza kadar sürdürebiliriz. Altın dikdörtgenlerin içine kısa kenarın ölçülerine göre kare odacıklar açtığımız sürece geriye yeni bir altın dikdörtgen kalacaktır.
Haydi bir kez daha...
Ve son! Burada duralım! Çünkü daha küçük altın dikdörtgenleri ortaya çıkarsak bile bunu göremeyeceğiz.
Şimdi en büyük kareden başlayıp, en küçük kareye kadar karelerin köşelerinden geçen bir yay çizelim ve bakalım ortaya ne çıkacak!..
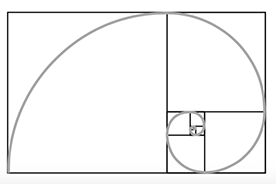
İşte bu! Evet bu kesinlikle yeryüzünde görülebilecek şekillerin en güzeli bir ALTIN SPİRAL ya da SARMAL!
İster teleskopla, ister mikroskopla isterse çıplak gözle bakıyor olalım onları her yerde görürüz: Hücrelerimizin içinde, uzayın derinliklerinde, birtakım tuhaf hayvanlarca içi boşaltılmış, terkedilip geride bırakılmış deniz kabuklarında, salyangoz evlerinde, taze asma uçlarında, kulağımızın ta en içinde, çam kozalaklarında, dağ keçilerinin ihtişamlı boynuzlarında görürüz...
Gözlerin hoşuna giden, bu adeta efsunlu şekil, sanki hiç tükenmeyecekmiş gibi kıvrıla kıvrıla dönen hatları ile insanın içinde, hiçbir şey uyandırmıyorsa bile bir devamlılık hissi uyandırır.
Kimbilir belki de bu yüzden sarmalları ilgi çekici buluruz, en çok ihtiyaç duyduğumuz, en çok arzuladığımız ve karşılığını Allah’tan başka hiç kimsenin veremeyeceği o olağanüstü duyguyu bize hissettirdiği için: sonsuzluğu!..

Fibonacci kimdir?
İtalyan Matematikçi Leonardo Fibonacci yaklaşık 1175 yılında Pisa şehrinde doğdu. Babası Filius Bonacci, Kuzey Afrika kıyılarındaki Bugia şehrinde (Bu şehir günümüzdeki Cezayir toprakları içinde yer alır ve Bjaiya adı ile bilinir) birtakım ticaret işleri ile meşguldü. Bu yüzden Leonardo, İtalyan yaşıtlarından farklı olarak eğitimini buradaki Berberî Müslüman hocalardan aldı.
Fibonacci’nin dostlarından biri, günlerden bir gün kendisine şöyle bir soru sormuş:
“Sevgili Fibo! Diyelim bir çift yavru tavşanım var. Bunlar iki ay sonra yavrulayacak hâle gelse ve biri kız diğeri erkek bir çift tavşan yavrulasa ve bu yavru çift tavşan da iki ay sonra yavrulayacak kadar büyüse ve büyüyen tavşanlar her ay bir çift tavşan yavrulasa ve tavşanlarım hiç ölmese bir yıl sonra kaç tavşanım olur?”
Soruyu anlaşıldı herhalde? Tavşanlar çabuk çoğalır bilirsiniz.

İsterseniz Ocak ayından itibaren tavşan çiftlerini hesap etmeye başlayalım:
OCAK: Sadece 1 çift tavşan yavrusu var elimizde.
ŞUBAT: Anne tavşan bebek bekliyor ama doğmamış tavşan sayılmıyor. Sayı hâlâ: 1
MART: İlk yavru çift doğdu. Sayı: 2
NİSAN: İlk çift artık büyüdüğüne göre her ay bir yavru çift doğabileceği için yeni bir çift yavru tavşan daha dünyaya geldi. Bir de geçen ay doğanlar vardı. Sayı: 3
MAYIS: İlk çift, bir çift daha dünyaya getirdi. İkinci çift büyüdüğü için onların da bir çift yavrusu dünyaya geldi. Geçen ay doğan henüz küçük bir çift daha vardı. Sayı: 5
HAZİRAN: Geçen ay doğan iki çift hariç diğer üç çiftin, birer çift tavşanı oldu. Sayı: 8
TEMMUZ: Geçen ay doğan üç çift hariç diğer beş çift tavşandan birer çift tavşan yavrusu dünyaya geldiği. Sayı: 13
Tavşanlar bu hızda üremeye devam ettiği sürece onların sayılarını hesap etmek giderek daha da zorlaşacağa benziyor. Şimdi ilk yedi ay için elde ettiğimiz sayıları sıralayayım:
1, 1, 2, 3, 5, 8, 13
Bu sayılara iyi bakın o vakit! Her biri kendinden önceki iki sayının toplamıdır. Ve eğer 8 ile 13’ü zihinden toplayabiliyorsanız, ağustos ayının tavşan çifti sayısının 21 olduğunu hemen söyleyebilirsiniz.
Hatta eylülü (21+13=34), hatta ekimi (21+34=55), hatta kasımı (34+55=89) ve yıl sonu olan aralığı (55+89=144)!..
İlk bir yılın, ay başına düşen tavşan çifti verilerini sıraladığımızda, şöyle bir sayı dizisi elde ederiz:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144
Her biri bir önceki iki sayının toplamının sonucu olan bu ilginç sayıların dizisine Fibonacci Sayıları adı verilir ve Fibonacci’nin anısına, matematik âleminde F ile gösterilir.





















